GLMM、GLMの解説
強化学習、機械学習の基礎的な知識は付いて来たと思ったので、
今度は確率統計よりの勉強をしています。
今回はこの本を軸に、GLMとGLMMの話を書きたいと思います。
本当は階層ベイズモデルやmcmc、stanなどの話まで持っていきたいのですが、
まだ理解できていないのでまたいつか。
さて、GLMは一般化線形モデルと呼ばれる手法で、データ分析などに用いられます。
具体的にはロジスティック回帰分析やポアソン回帰と呼ばれる手法が該当します。
確率分布、リンク関数、線形予測子の3つを指定することにより決定する統計モデルです。
ロジスティック回帰分析を例にして、説明していきたいと思います。

上記画像の右のグラフを見てみてください。
このような散布図から、ロジスティック曲線を引くことにより、データを予測分析するのがロジスティック回帰分析です。
リンク関数は、散布図の形状に合うようなものを指定します。散布図が「/」のような形になっていることから、リンク関数はロジスティック関数を選んで問題なさそうです。
また、各xの値に対応する縦軸の点の分布から、確率分布を決定します。今回は正答数という離散値の分布なので二項分布にします。
線形予測子とは、ロジスティック関数のzに対応する値です。説明変数と応答変数を紐づけるような役割を担っています。そして、今回は説明変数が児童の年齢だけなので、線形予測子として「z=b_1 + b_2 x_i」としましょう。

上記のb_1とb_2を求めることができれば、ロジスティック回帰分析を行うことができます。

この式から最尤推定を行うことにより求めます。
このようにGLMは確率分布、リンク関数、線形予測子の3つからなります。
しかし、問題点があって、過分散という状況に対応することができません。

過分散とは右のグラフのように、中央値に対して分散が大きすぎて、散布図が「U」のような形になることです。二項分布と散布図がマッチしていないことが分かるかと思います。
これに対応するためのものがGLMMです。


このように線形予測子に、ある確率分布から生成される変数を加えます。
この変数は個体差などと呼ばれ、個体間の差を統計モデルに組み込むことができるようになります。
先ほどのGLMと比べて、パラメータがb_1,b_2,sの3つになりましたね。
これも先ほどと同様に、最尤推定により求めることができます。

ここの積分計算の過程が理解しにくいかと思いますが、
下のURLのアニメーションが大変わかりやすいです。
http://yagays.github.io/blog/2012/11/09/glm-mcmc-chp7-2/
過分散を表せていることが分かるかと思います。
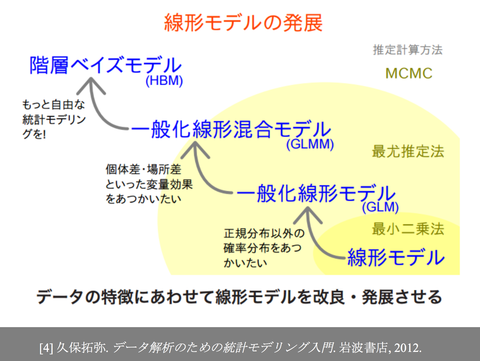
今回はGLMとGLMMについて説明しました。
これをさらに発展させると階層ベイズモデルになります。
GLMMは全てのデータから尤度が最大になるように学習する仕組みですが、
こいつにベイズの定理を持ち込むことにより、逐次的に学習を行えるようにしたのが階層ベイズ学習のようです。
GLMやGLMM、階層ベイズモデルはRでstanというライブラリを使うのが一般的なようです。
こちらの本が詳しいようですね。
購入してまだ読んでいないので、またやっていこうかと思います。

